728x90
반응형
1. 개요
앞서서 정보이론의 중요 개념들을 살펴봤고 이제는 이를 패턴인식에 연결시키고자 합니다.
2. 내용
- 어떤 알려지지 않은 분포 p(x)가 있고, 우리는 이를 근사화한 분포 q(x)를 사용하여 모델링했다고 가정해 봅시다.
만일 우리가 q(x)를 수신자에게 x값을 전달하는 목적으로 코딩 전략을 짜는데 사용한다면, p(x) 대신 q(x)를 사용하므로서 x를 구체화하기위해 필요한 평균적인 추가 정보량 (in nats)은 수식 1.113과 같습니다. 이를 분포 p(x)와 q(x) 간의 상대 엔트로피 (relative entropy) 혹은 Kullback-Leibler divergence, 또는 KL divergence라고 합니다. 여기서 알아둘 점은, KL(p||q)와 KL(q||p)는 대칭적으로 항상 같은 것은 아닙니다.

- KL(p||q) >= 0을 충족하며 0과 같을 때는 p(x) = q(x)일 때입니다. 이것을 보이기 위해서는 컨벡스 (convex) 함수의 개념을 도입해야 합니다. 함수가 컨벡스 하다는 것은 각 현(chord)이 함수 위에 또는 그 위에 위치하는 특성이 있다는 것입니다. 이는 1.31번 그림에 나타나 있습니다.
현 (chord) : 곡선 위의 두 지점을 잇는 선

- x=a에서 x=b까지의 어떤 간격에 있는 x는 lambda*a + (1-lambda)*b로 표현할 수 있습니다. 여기서 0 =< lambda =< 1입니다. 현 (chord)에 상응하는 지점은 lambda*f(a) + (1-lambda)*f(b)로 주어집니다.
함수의 상응하는 값은 f(lambda*a+(1-lambda)*b) 입니다. 그러면, 컨벡스성 (convexity)는 수식 1.114를 암시하게 됩니다.

- 이것은 함수의 2차 미분 계수가 어떤 곳이든 양수야 한다는 조건과 마찬가지입니다. 컨벡스 함수의 예수는 xlnx (for x>0)과 x**2입니다. lambda = 1과 lambda = 0에 대해서만 동등함 (equality)가 성립할 때는 해당 함수는 엄격하게 컨벡스 (strictly convex)라고 합니다. 만일 이와 반대의 성질로 모든 현이 함수에 있거나 밑에 있다면 이를 컨케이브 (concave) 라고 하며 앞의 것과 상응하는 정의를 엄격하게 컨케이브 (strictly concave)라고 합니다. 만일 f(x)가 컨벡스라면 -f(x)는 컨케이브입니다.
- 이를 이용하면 수식 1.114로부터 컨벡스 함수 f(x)는 수식 1.115를 만족하는 것을 보일 수 있습니다.
여기서 모든 점 {x_i}에 대해 lambda_i >=0 이고 sigma[labmda_i]=1이며 입니다.
수식 1.115는 젠센의 부등식 (Jensen's inequality)라고 알려져 있습니다.

- 만일 lambda_i를 {x_i}에 있는 이산 변수 x에 대한 확률 분포로서 해석한다면 수식 1.115는 수식 1.116으로 바뀝니다.
여기서 E[*]는 기대값을 의미합니다.

- 연속적인 변수들에 대해 젠센의 부등식은 수식 1.117로 표현됩니다.

- 수식 1.117을 KL divergence (수식 1.113)에 적용하면 수식 1.118을 얻을 수 있습니다.
여기서 -lnx는 컨벡스 함수란 사실과 표준화 조건인 integral_[q(x)]dx = 1을 이용했습니다. 사실 -lnx는 엄격한 컨벡스 함수입니다. 따라서 동일함 (equality)는 모든 x에 대해 q(x) = p(x)일 때만 충족됩니다. 따라서, KL divergence를 p(x)와 q(x)의 비유사도 (measure of dissimilarity)로 해석할 수 있습니다.

- 여기서 데이터 압축과 밀도 예측 간의 관계를 알 수 있습니다. 다시 말해, 알지 못하는 확률 분포를 모델링하는 문제입니다. 그러한 이유는 가장 효율적인 압축은 우리가 진짜 분포를 알고 있을 때 달성 할 수 있기 때문입니다. 만일 우리가 실제 분포와 다른 분포를 사용한다면, 우리는 덜 효과적인 코딩을 할 수 밖에 없습니다. 그리고 반드시 전달되어야할 추가적인 정보량은 평균적으로 (최소한) 두 분포 사이의 KL divergence와 같습니다.
- 우리가 알지 못하는 분포 p(x)를 몇 가지 조정 가능한 파라미터 (theta)로 이루어진 q(x|theta)로 모델링해서 근사하고 싶다고 해봅시다. theta를 결정하는 한 가지 방법은 p(x)와 q(x|theta)간의 KL divergence를 최소화 시키는 theta를 구하는 것입니다. 우리는 p(x)를 알지 못하기 때문에 직접할 수는 없습니다. 그러나, 우리가 유한 개의 훈련 데이터 x_n이 있다고 해봅시다. 여기서 n은 1부터 N까지이며 p(x)를 따릅니다. 이렇게하면 p(x)에 대한 기대값은 수식 1.35를 사용해서 유한 개의 훈련데이터의 합으로서 근사할 수 있습니다. 이리하면 수식 1.119와 같이 나옵니다.

- 수식 1.119의 우변의 두 번 째항은 theta에 독립적입니다. 그리고 첫번 째 항은 theta에 대해 음수 로그 가능도 함수 (negative log likelihood function)으로 q(x|theta)의 분포를 따르며 해당 분포는 훈련데이터로 평가됩니다. 따라서, KL divergence를 최소화 시킨다는 것은 가능도 함수를 최대화시키는 것과 등치입니다.
- 이제 x와 y 변수들로 이루어진 2개 집합 간의 결합 분포 (joint distribution) p(x,y)를 고려해봅시다. 만일 변수들 간에 독립이라면 그것들의 결합 분포는 p(x,y) = p(x)p(y)가 될 것입니다. 만일 그러지 않다면, 그것들이 독립이기에 가까운지를 KL divergence를 고려하여 알아볼 수 있습니다 (수식 1.120).
이 수식 1.1120을 x와 y간의 상호의존정보 (mutual information)라고 합니다.
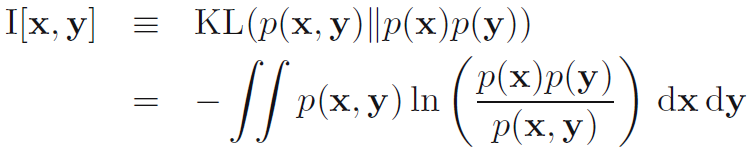
- KL divergence의 특징들로부터 I(x,y)>=0이란 것을 알 수 있고 0일 때는 오로지 x와 y가 독립일 때란 것을 알 수 있습니다. 확률 덧셈과 곱셈 법칙을 사용해서 상호의존정보는 조건부 엔트로피와 연관된 것을 수식 1.121로 나타낼 수 있습니다. 따라서 상호 정보를 x의 불확실성 감소로 볼 수 있습니다. y의 값을 알게 됨으로써 (또는 그 반대로) x에 대한 불확실성이 어떻게 감소하는지에 대한 것입니다.
베이지안 관점에서는 p(x)를 x에 대한 사전분포 (prior distribution)로 p(x|y)는 새로운 데이터 y를 관측한 후의 사후 분포 (posterior distribution)로 볼 수 있습니다. 따라서, 상호의존정보는 새로운 관측값 y의 결과로서 감소하는 x에 대한 불확실성으로 표현됩니다.

728x90
반응형
'DeepLearning > Pattern recognition and Machine learning' 카테고리의 다른 글
| [PRML] 2.1. Binary variables (이진 변수들) (0) | 2024.02.01 |
|---|---|
| [PRML] 2. Probability distributions (확률 분포들) (0) | 2024.01.26 |
| [PRML] 1.6. Information theory (정보 이론) (0) | 2024.01.15 |
| [PRML] 1.5.5 Loss functions for regression (회귀에 대한 손실함수들) (0) | 2024.01.12 |
| [PRML] 1.5.4 Inference and decision (추론과 결정) (0) | 2024.01.11 |


