728x90
반응형
1. 개요
먼저, 단일 이진 무작위 변수 (single binary random variable) x ∈ {0,1}에 대해 다루면서 시작하겠습니다. 예를들어 x는 동전 던지기로 설명할 수 있습니다. x=1은 앞 면 (heads) x=0은 뒷면 (tails)로 기술하는 것이지요.
2. 내용
- 동전이 손상되어서 앞 면이 떨어질 확률이 뒷 면이 떨어질 확률과 다르다고 상상해봅시다. 그렇다면 x=1의 확률은 파라미터 u에 대해 수식 2.1과 같이 표기됩니다. 여기서 0<=u<=1이며 p(x=0|u) = 1-u를 따릅니다.
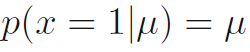
- x에대한 확률 분포는 수식 2.2로 표기됩니다. 이것은 베르누이 분포 (Bernoulli distribution)로 알려져 있습니다

- 이것의 평균과 분산은 수식 2.3과 수식 2.4로 표기됩니다.

- 이제 데이터셋 D = {x_1, ...., x_N}이 관측된 x에 대한 집합으로 있다고 합시다. 관측값들은 p(x|u)로부터 독립적으로 추출됐다고 가정하고 u에 대한 가능도 함수를 만들면 수식 2.5와 같습니다.

- 빈도주의 관점에서, u의 값을 가능도 함수를 최대화 하거나 혹은 로그함수를 최대화 하는 것으로서 예측할 수 있습니다. 베르누이 분포에서는 로그 가능도 함수는 수식 2.6으로 나타납니다.

- 이 시점에서, 로그 가능도 함수는 N개의 관측값들 x_n에만 의존한다는 것을 그것들의 합 sigma[x_n]이라는 것을 알 수 있습니다. 이 합은 이 분포에서의 데이터에 대한 충분한 통계치 (sufficient statistic)의 예를 제공합니다. 추후에 다른 몇 가지 중요한 충분한 통계치에 대해 공부할 것입니다. 만일 우리가 ln[p(D|u)]에 대해 미분을 하고 u를 0으로 만들게 한다면, 최대 가능도 에측 (maximum likelihood estimator)는 수식 2.7로 나옵니다. 이 수식 2.7은 샘플의 평균 (sample mean)입니다.

- 만일, 데이터셋 내의 x=1 (head)에 대한 관측값들의 수를 m으로 표기한다면 수식 2.7을 수식 2.8로 변경할 수 있습니다. 이를 통해 앞면이 떨어질 확률은 데이터셋 내의 앞면 관측의 비율로 표기됩니다.

- 이제 만일 우리가 3번 던졌더니 3번 모두 앞면이라고 해봅시다. 그러면 N=m=3이므로 u_ML=1이됩니다. 이 경우, 최대 가능도 결과는 모든 미래 관측값들을 앞면으로 줄 것입니다. 상식적으로 이것은 이성적이지 않으며 이것은 실제로 최대 가능도의 과적합 (over-fitting associated with maximum likelihood)의 극단적인 예입니다. 이것에 대한 좀 더 합리적인 결론들은 u에 대한 사전확률 분포를 도입함으로서 어떻게 도달할 수 있는지 곧 다룰 것입니다.
- x=1이라는 관측값들의 숫자 m에 대한 분포를 N개의 데이터셋에 대해 분포를 설정해서 고려할 수 있습니다. 이것을 이항 분포 (binomial distribution)이라고 합니다. 그리고 이것은 [u**m][(1-u)**(N-m)]에 비례합니다.
표준화 상수 (normalization coefficient)를 얻기 위해, N번의 시행 시에 m번의 앞면에 대한 가능한 모든 경우를 합쳐야합니다. 그래서 이항분포는 수식 2.9와 같이 적힙니다. 여기서 (N m)은 수식 2.10과 같습니다. 수식 2.10은 N개에서 m개의 물체를 선택하는 가능한 수를 의미합니다.


- 그림 2.1은 N = 10에 대해 u = 0.25일 때의 이항분포를 보여줍니다.

- 이항분포에서는 독립적인 사건들에 대한 합의 평균은 평균의 합과 같으며 합들의 분산은 분산의 합과 동일합니다. 왜냐하면 m = x_1 + ... + x_N에 대해 각각의 관측에 대한 평균과 분산은 수식 2.3과 2.4로 주어지며 이를 통해 수식 2.11과 수식 2.12를 얻습니다. 이것들은 미분을 활용하면 직접 증명이 가능합니다.

728x90
반응형
'DeepLearning > Pattern recognition and Machine learning' 카테고리의 다른 글
| [PRML] 2.2. Multinomial variables (다변량 변수) (0) | 2024.02.27 |
|---|---|
| [PRML] 2.1.1 The beta distribution (베타 분포) (0) | 2024.02.06 |
| [PRML] 2. Probability distributions (확률 분포들) (0) | 2024.01.26 |
| [PRML] 1.6.1 Relative entropy and mutual information (상대 엔트로피와 상호 의존 정보) (0) | 2024.01.23 |
| [PRML] 1.6. Information theory (정보 이론) (0) | 2024.01.15 |


