728x90
반응형
1. 개요
- 패턴 인식의 분야에서 중요한 개념 중 하나는 불확실성 (uncertainty)이다.
이것은 노이즈나 유한한 데이터 크기 등 다양한 원인으로 생길 수 있다. - 확률 이론은 불확실성에 대한 측정 (quantification)과 조절 (manipulation)을 위한 일관된 뼈대를 제공한다.
비록 불완전하거나 애매할 수 있지만, 이것이 결정이론 (decision theory, 챕터 1.5)와 결합되면 활용가능한 모든 주어진 정보에 대해 적절한 예측을 가능하게 해준다.
2. 내용
- 예시로 빨강 상자에는 사과 2개와 오렌지 6개가 있고 파랑 상자에는 사과 3개와 오렌지 1개가 있다. 여기서 무작위로 박스를 선택한 후, 무작위로 과일을 고른 후 다시 해당 상자에 돌려 넣는 과정을 수 많이 반복해보자. 이랬을 때, 빨강 박스가 40%이고 파랑 박스가 60% 선택됐고 어떤 과일을 선택할 확률은 동일하다고 가정해 봅시다.
- 이 예제에서 어떤 상자를 선택하는 무작위 변수를 B라 하고 빨강이면 r 파랑이면 b로 표기하고 과일을 선택할 무작위 변수는 F이고 사과는 a 오렌지는 o로 표기합시다. 상자들의 확률은 아래와 같이 표기가 가능합니다.
p(B = r) = 4/10, p(B = b) = 6/10
확률은 반드시 0이상 1이하의 값 [1, 0] 안에 들어와야 합니다. - 이 때, '사과를 하나 뽑게될 전반적인 확률값은 무엇인가?' 같은 문제를 풀 때 필요한 확률 규칙은 2가지입니다.
- 합 규칙 (sum rule)
- 곱셈 규칙 (product rule)

합규칙과 곱셈규칙 수식
- 위의 예제를 보다 일반적인 용어로 변경하면 그림과 같이 X와 Y라는 무작위 변수가 관여하는 상황으로 나타낼 수 있음. 여기서, X는 1~M까지 중 원소 i를 선택할 수 있는 것이고 Y는 1~L까지 중 원소 j를 선택하며 이 경우들을 각각 xi와 yj로 나타냄. 그리고 Y와 상관없이 특정 xi가 발생하는 시행횟수를 ci라 두고 X와 상관없이 특정 yj가 발생하는 시행횟수를 rj라고 둠. 이 경우의 확률은 p(X=xi, Y=yj)로 둘 수 있으며 이를 X=xi와 Y=yj의 동시 확률 (joint probability)라고 부름. 이것은 아래의 수식으로 나타냄. 아래 수식에서 nij는 xi와 yj가 동시에 생겼던 횟수를 의미하며 N은 전체 시행횟수를 의미함.

- N이 무한대일 때 xi의 확률은 그림의 행렬에서 i가 차지하는 부분 (fraction)이 되며 그 값은 아래의 수식과 같음.
이것이 확률의 합규칙 (sum rule)임. 종종 p(X=xi)는 다른 변수들의 의미를 줄여버린다 (marginalizing)는 의미에서 주변확률 (marginal probability)라고 불리기도함.
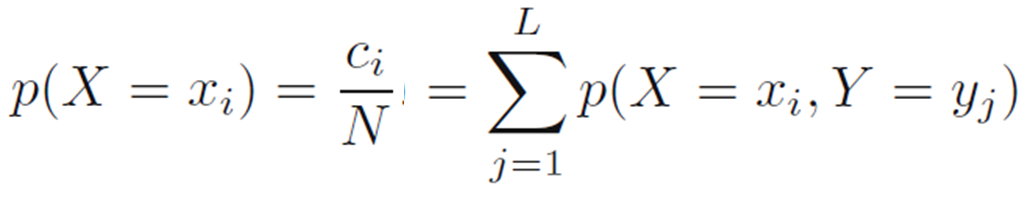
- 만일 X=xi의 조건에서 Y=yj가 얼만큼 차지하는지를 볼 때는 p(Y = yj | X = xi)라고 표기하며 이는 X = xi에 대해 Y = yj의 조건부 확률 (conditional probability of Y = yj given X = xi)라고 합니다. 일반적으로 Y=yj는 생략하고 p(Y)로 표기합니다.

- 위의 식들을 통해 아래의 관계를 유도할 수 있는데 이를 곱셈 규칙 (product rule)이라 합니다.
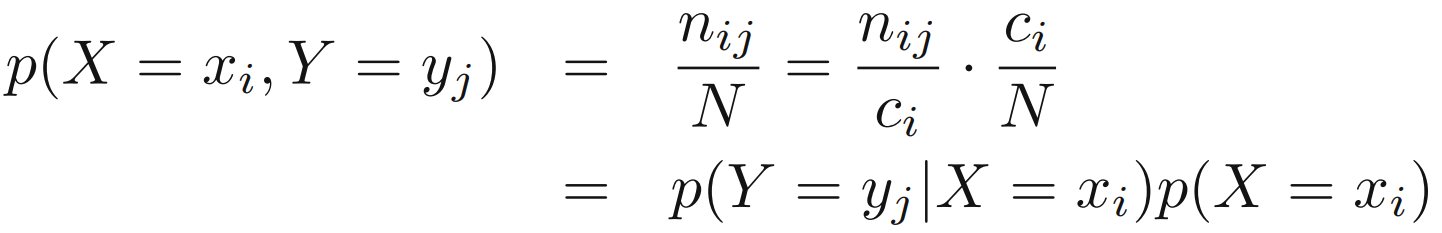
- 곱셈규칙과 p(X,Y)=p(Y,X)라는 대칭성을 이용해서 조건부 확률간의 관계를 도출할 수 있습니다.
이를 베이즈 정리 (Bayes' theorem)이라 하며 패턴 인식과 기계학습에서 중요한 역할을 합니다.

- 합 규칙을 사용하면 베이즈 정리의 분모는 분자에 나타나는 양으로 표현될 수 있습니다.
(Using the sum rule, the denominator in Bayes’ theorem can be expressed in terms of the quantities appearing in the numerator)

- 이러한 방식을 사용하면 베이즈 정리의 분모는 모든 Y 값에 대한 조건부 확률의 합이 1이 되도록 보장하는 데 필요한 정규화 상수로 볼 수 있습니다.
- 앞에서 나온 베이즈 정리를 이용해 사과가 나올 확률을 다음과 같이 유도할 수 있음.
오렌지는 1-p(F=a)를 하면 나오게 됨.

- 위의 상황과 달리 우리가 뽑은게 오렌지인데 이것이 어디 상자에서 온 것인지 알고 싶을 수가 있음. 이것은 확인된 과일에 대한 상자들의 확률 분포를 고려해야하는 것임. 이것을 베이즈 정리로 유도하면 아래와 같음.
합 규칙에 따라서 파란색 상자는 1-p(B=r|F=o)가 됨.

- 만일 우리가 과일의 정체를 듣기 전에 어떤 박스가 선택됐을지 질문을 받는다면, 가장 완전한 정보는 p(B)값임. 이것을 사전확률 (prior probability)라고 부름. 이유는 우리가 과일의 정체를 보기 전에 이용 가능한 확률이기 때문임.
(We call this the prior probability because it is the probability available before we observe the identity of the fruit.) - 우리가 그 과일은 오렌지였다고 듣게되면, 베이즈 정리를 활용해 p(B|F)값을 산출할 수 있음. 이를 사후확률 (posterior probability)라고 부름. 이유는 우리가 과일 (Fruit)을 관측한 후에 얻어지는 확률이기 때문임.
(p(B|F), which we shall call the posterior probability because it is the probability obtained after we have observed F.) - 마지막으로, 두 변수의 동시 분포 (joint distribution)이 주변확률의 곱셈값과 동일하다면, 즉 p(X,Y) = p(X)p(Y)인 경우, X와 Y는 독립 (independent)이라고 불림.
(if the joint distribution of two variables factorizes into the product of the marginals, so that p(X,Y) = p(X)p(Y), then X and Y are said to be independent.) - 곱셈 규칙으로부터 이 경우에는 p(Y|X) = p(Y)가 성립됨. 예를들어, 앞선 과일과 상자 예시에서 각 상자가 동일한 비율의 사과와 오렌지를 갖고 있다면 p(F|B)는 p(F)가 됨.
추가 사항
- 여기선 우도/가능도 (likelihood)에 대해선 안나왔는데 P(F|B)가 가능도이다. 이것은 해당 박스에서 오렌지가 선택될 확률 (가능한 확률)을 의미한다.
728x90
반응형
'DeepLearning > Pattern recognition and Machine learning' 카테고리의 다른 글
| [PRML] 1.2.3 Bayesian probabilities (베이지안 확률들) (0) | 2023.11.07 |
|---|---|
| [PRML] 1.2.2 Expectations and covariances (기대값과 공분산) (0) | 2023.11.06 |
| [PRML] 1.2.1 Probability densities (확률 밀도) (0) | 2023.11.03 |
| [PRML] 1.1 Example: Polynomial Curve Fitting (0) | 2023.10.10 |
| [PRML] 1. introduction (0) | 2023.10.04 |


