728x90
반응형
1. 개요
수식 2.8에서 봤듯이 베르누이 분포와 나아가 이항 분포에서 u에대한 최대 가능도 설정은 데이터에서 x=1이라는 값을 갖는 관측값의 비율이다. 이것은 이미 말했듯이 과적합 문제를 작은 데이터셋에서 발생시킬 수 있다.
이 문제에 대해 베이지안 해결법을 적용하기 위해서는 우리는 u에대한 사전확률 p(u)를 도입해야 한다. 여기서 우리는 간단하고 유용한 분석적인 특징을 갖는 사전확률의 한 가지 형태를 고려할 것이다.
2. 내용
- 가능도 함수는 [u**x][(1-u)**(1-x)]의 형태의 원소들의 곱셈으로 이루어진다는 것을 알고 있다. 만일 우리가 사전확률이 u와 (1-u)의 승수 (powers of u and 1-u)에 비례하는 사전확률을 선택한다면, 사전확률과 가능도 함수에 비례하는 사후 확률 분포는 사전확률과 같은 형태의 함수 형태를 가질 것이다. 이런 특징을 켤레 (conjugacy)이라고 한다.
- 따라서, 우리는 사전확률을 베타분포 (beta distribution)이라는 수식 2.13으로 정의 되는 것으로 고를 것이다.
여기서 gamma(x)는 감마 함수로 수식 1.141에 정의되어 있으며 수식 2.13안의 계수 (coefficient)는 베타 분포가 표준화되게해준다. 이를 통해 수식 2.14가 성립한다.



- 베타분포의 평균과 분산은 수식 2.15와 수식 2.16과 같습니다.
파라미터 a와 b는 하이퍼파라미터 (hyperparameters)라고 합니다. 왜냐하면 그것들은 파라미터 u의 분포를 조절하기 때문입니다. Figure 2.2는 이 하이퍼파라미터들에 따른 베타 분포들이 어떻게 변화하는지 보여줍니다.


- u의 사후확률 분포 (posterior distribution of u)는 베타 사전확률 (beta prior, 수식 2.13)을 이항 가능도 함수 (수식 2.9)에 곱하고 표준화 시켜서 얻을 수 있습니다. u에 의존적인 요소들 (factors)만 남기면 사후확률분포는 수식 2.17과 같이 나옵니다. 여기서 l = N - m이며 이는 동전 예제에서는 뒷면 (tails)의 숫자에 대응됩니다.

- 수식 2.17 식이 사전 분포와 동일한 형태로 매개 변수 μ에 의존한다는 것을 볼 수 있습니다. 이는 가능도 함수에 대한 사전 분포의 켤래 특성 (conjugacy properties of the prior)을 반영합니다. 실제로, 이것은 단순히 다른 베타 분포입니다. 그리고 이것의 표준화 상수는 수식 2.13과 비교해서 수식 2.18로 얻을 수 있습니다.

- 우리는 사전 분포에서 사후 분포로 이동하는 과정에서 x=1인 m개의 관측들과 x=0인 l 개의 관측들로 이루어진 데이터셋이 a라는 값을 m만큼 증가시키고 b는 l만큼 증가시키는 것을 볼 수 있습니다. 이는 사전 분포의 매개변수 a와 b를 x=1 및 x=0에 대한 효과적인 관측 횟수 (effective number of observations)로 간단하게 해석할 수 있게 해줍니다. 여기서 a와 b는 정수 (integers)일 필요는 없습니다.
- 우리가 만일 추가적인 데이터를 관측한다면 사후분포는 사전분포처럼 행동할 수 있습니다. 이를 확인하기 위해, 우리가 어떤 관측들을 한 개씩 보면서 그 때마다 현재의 사후확률을 업데이트를 진행한다고 해봅시다. 그 업데이트 방식은 사후확률을 새로운 관측의 가능도 함수에 곱하고 표준화시키는 것입니다. 각 단계에서, 사후분포는 파라미터 a와 b로 주어지는 x=1과 x=0인 관측값들의 어떤 값 (사전분포와 실제값)에 대한 베타 분포를 띨 것입니다. x=1에대한 추가적인 관측값의 추가는 간단히 a를 1만큼 증가시키는 것에 상응합니다. 반면, x=0의 경우는 b를 1만큼 증가시키는 것입니다. 그림 2.3은 이 과정을 그리고 있습니다.

- 이러한 순차적인 접근법 (sequential approach)은 베이지안 시점을 적용했을 때 자연스럽게 생긴다는 것을 알 수 있습니다. 이것은 사전확률의 선택과 가능도 함수와 상관없지만 i.i.d. 데이터라는 가정에는 의존적입니다. 순차적인 방법들은 관측값들을 한 번에 하나 씩 또는 작은 배치들로 고려합니다. 그리고 그것들은 다음 관측값들을 사용되기 전에 버려집니다. 예를들어, 이것들은 데이터가 꾸준하게 입력되고 모든 데이터를 보기 전에 예측을 해야하는 실시간 학습 시나리오들에서 사용될 수 있습니다. 이것들은 메모리에 저장하거나 로딩된 상태일 필요는 없으므로 순차적인 방법들은 매우 큰 데이터셋에 유용합니다. 최대 가능도 방법들도 순차적인 작업방식에 적용이 가능합니다.
- 만일, 우리의 목표가 새로운 시행에서의 결과가 무엇일지 예측하는 것이라면, 주어진 관측된 데이터셋 D에대해 (given the observed dataset D) x의 예측 분포에 대해 반드시 평가를 해야합니다. 확률의 합과 곱셈법칙에 따라, 수식 2.19를 유도할 수 있습니다.

- 사후 확률분포 p(u|D)에대해 수식 2.18을 사용하면서 베타분포의 평균에 대한 수식 2.15를 함께 이용하면 수식 2.20을 얻을 수 있다. 수식 2.20은 x = 1에 상응하는 관측값들 (실제 관측값과 가상의 사전 관측값 (fictitious prior observations)들) 에 대한 전체적인 비율에 대한 간단한 해석을 제공한다. 여기서, m과 l이 매우 큰 데이터라면 수식 2.20은 최대가능도 결과 (수식 2.8)에 수렴하게 된다.
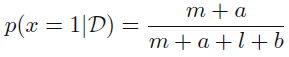
- 유한한 데이터셋의 경우 u에 대한 사후 평균 (posterior mean)은 항상 사전 평균 (prior mean)과 2.7에 주어진 상대적인 빈도에 상응하는 u에 대한 최대 가능도 예측값 사이에 위치한다.
For a finite dataset, the posterior mean for u always lies between the prior mean and the maximum likelihood estimate for u corresponding to the relative frequencies of events given by 2.7. - 그림 2.2에서 관측값이 증가함에 따라 사후확률 분포가 뾰족하게 생겨가게 되는 것을 볼 수 있다. 이것은 베타 분포의 분산에 대한 수식 2.16에서 확인할 수 있는 것이다. 해당 수식에서 a와 b를 무한 대로 보내게 되면 분산이 0으로 수렴하는 것을 볼 수 있다.
- 일반적으로 베이지안 학습의 특징이 많은 데이터를 제공할수록 사후 분포에서 나타나는 불확실성이 꾸준히 감소한다. 데이터셋 D에 대해 파라미터 theta를 유추하는 일반적인 문제를 가정해보자. 이 결합분포는 p(theta,D)로 표현된다. 그리하면 수식 2.21이 나오는데 오른쪽 항의 기호들은 수식 2.22와 수식 2.23과 같다.


- 이것은 theta의 사후평균 (데이터를 생성하는 분포에 대한 평균)은 theta의 사전펴육ㄴ과 동일하다는 것을 보여준다. 비슷하게 수식 2.24를 보일 수 있다. 수식 2.24의 좌변은 theta의 사전분산이다. 우변의 첫 번째 항은 theta의 평균 사후 분산이며 두 번째 항은 theta의 사후확률의 분산을 나타낸다. 이 분산은 양의 값이기 때문에, 이 결과는 theta의 사후분산은 사전분사보다 일반적으로 작다는 것을 보여준다. 분산의 감소는 사후 평균의 분산이 클수록 커진다. 하지만, 이 결과는 어디까지나 평균적으로 그렇다는 것이며 특정한 데이터셋에서는 사전 분산보다 사후 분산이 더 클 가능성이 있다.

728x90
반응형
'DeepLearning > Pattern recognition and Machine learning' 카테고리의 다른 글
| [PRML] 2.2.1 The Dirichlet distribution (디리클레 분포) (0) | 2024.03.04 |
|---|---|
| [PRML] 2.2. Multinomial variables (다변량 변수) (0) | 2024.02.27 |
| [PRML] 2.1. Binary variables (이진 변수들) (0) | 2024.02.01 |
| [PRML] 2. Probability distributions (확률 분포들) (0) | 2024.01.26 |
| [PRML] 1.6.1 Relative entropy and mutual information (상대 엔트로피와 상호 의존 정보) (0) | 2024.01.23 |


