1. 개요
오토 인코더 (autoencoder)는 어떤 사물의 특징을 좀 더 작은 차원으로 압축하는 인코더와 작은 차원에서 원래의 특징으로 복원하는 디코더 (decoder)로 이루어져 있다. 오토인코더는 자신이 학습한 것만을 잘 압축하고 잘 복구할 수 있기 때문에 학습이 된 적이 없는 사물이 주어지면 재복원 오차 (reconstruction error)값이 크게 나온다. 이를 활용해 이상치를 탐지에 이용할 수 있다.
하지만, 오토인코더가 종종 모든 사물을 잘 압축하고 잘 복원할 수 있는 경우가 생길 수 있다. 이러한 문제를 해결하기 위해 오토인코더를 학습한 후에 정상 데이터에 대한 특징을 저장하는 모듈 (memory module)을 만들어서 좀 더 견고한 이상치 탐지를 할 수 있다.
2. 원리
방식은 정상치 데이터에 비해 굉장히 작은 양의 메모리 슬롯 (memory slot)을 만드는 것이다. 예를들어 mnist는 훈련용 데이터가 6만 개인데 저자들은 100개의 슬롯 (즉, 정상에 대한 기억 100개)로 만들었다. 학습이 진행되면서 메모리는 정상에 대한 어렴풋한 이미지를 만들어가게 된다.
새로운 사물이 들어오면 인코더를 통해 특징이 압축된 벡터가 생성된다. 이후에, 이것과 가장 유사한 벡터를 코사인 유사도 (cosin similarity)로 계산한 후 소프트맥스 (softmax)로 확률값으로 변환해준다. 이후에 적절한 기준값을 적용해 기준값에 미달한 기억들은 제외하고 상위에 해당하는 메모리들의 차원과 확률값을 곱해서 만들어진 벡터로 디코더에 집어 넣어 복원한다.
이 과정을 잘 거치면 전통적인 오토인코더보다 좀 더 나을 수도 있다. 내가 해봤을 때는 항상 그런 것은 아니었고 mnist에서는 특정 숫자만 잘됐다.
3. 코드
# mnist 데이터를 불러온다.
import sys, os
import torch, torchvision
params={
'workdir':'/path/to/working/directory'
,'datadir':'/path/to/mnist'
}
indata={}
indata['mnist']=torchvision.datasets.MNIST(root=params['datadir'],download=0)
indata['mnist-test'] = torchvision.datasets.MNIST(root=params['datadir'], train=False, download=True, transform=None)
# 실습에 사용할 인코더의 형태
import torch.nn as nn
class encoder(nn.Module):
def __init__(self,indim,outdim):
super(encoder,self).__init__()
self.indim=indim
self.outdim=outdim
self.fc_layer = nn.Sequential(
nn.Linear(self.indim, 392,bias=False),
nn.BatchNorm1d(392),
nn.LeakyReLU(),
nn.Linear(392, 256,bias=False),
nn.BatchNorm1d(256),
nn.LeakyReLU(),
nn.Linear(256, 128,bias=False),
nn.BatchNorm1d(128),
nn.LeakyReLU(),
nn.Linear(128, self.outdim,bias=False),
nn.BatchNorm1d(self.outdim),
nn.LeakyReLU(),
)
def forward(self,_input):
out=self.fc_layer(_input)
return out
E=encoder(indim=int(28*28),outdim=64)# 디코더의 형태
import torch.nn as nn
class decoder(nn.Module):
def __init__(self,indim,outdim):
super(decoder,self).__init__()
self.indim=indim
self.outdim=outdim
self.fc_layer = nn.Sequential(
nn.Linear(self.indim, 128,bias=False),
nn.BatchNorm1d(128),
nn.LeakyReLU(),
nn.Linear(128, 256,bias=False),
nn.BatchNorm1d(256),
nn.LeakyReLU(),
nn.Linear(256, 512,bias=False),
nn.BatchNorm1d(512),
nn.LeakyReLU(),
nn.Linear(512, self.outdim,bias=False),
nn.BatchNorm1d(self.outdim),
nn.LeakyReLU(),
)
def forward(self,_input):
out=self.fc_layer(_input)
return out
D=decoder(indim=64,outdim=int(28*28))
# 정상 데이터 설정
# 아래의 예시에서는 숫자 2를 정상치로 설정했다.
def select_normal_dataset(dataset='train',num=2):
'''
num = 정상값으로 지정될 데이터셋.
'''
if dataset=='train':
td=indata['mnist'].train_data/255 # scaling 0~1
td_idx=indata['mnist'].train_labels
print(dataset,len(td))
else:
td=indata['mnist-test'].test_data /255 # scaling 0~1
td_idx=indata['mnist-test'].test_labels
print(dataset,len(td))
# Get normal dataset
normal_idx=[i for i in range(len(td_idx)) if td_idx[i]==num]
normal_td=td[normal_idx,:]
anormal_idx=list(set(list(range(len(td_idx))))-set(normal_idx))
anormal_idx.sort()
anormal_td=td[anormal_idx,:]
return {'Normal':normal_td,'Anormal':anormal_td}
pdata={}
pdata['train-dataset']=select_normal_dataset(num=2)
pdata['test-dataset']=select_normal_dataset(dataset='test',num=2)# 훈련 파라미터 설정
epoch=1000
batch_size=1024
E=encoder(indim=784,outdim=64)
D=decoder(indim=64,outdim=784)
device=0
import torch.optim as optim
optimizerE=optim.Adam(E.parameters())
optimizerD=optim.Adam(D.parameters())
import torch.functional as F
criterion=torch.nn.MSELoss()# 오토인코더 학습 진행
loss_track=[]
E.train();D.train()
from tqdm import tqdm
E.to(f'cuda:{device}');D.to(f'cuda:{device}')
for e in tqdm(range(epoch)):
train = torch.utils.data.DataLoader(pdata['train-dataset']['Normal'], batch_size=batch_size,shuffle=True,drop_last=True)
loss_total=0
for t in train:
t=t.to(f'cuda:{device}').view(batch_size,-1)
fake_t=D(E(t))
loss=criterion(t,fake_t)
optimizerE.zero_grad()
optimizerD.zero_grad()
loss.backward()
optimizerE.step()
optimizerD.step()
loss_total+=loss.item()
loss_track.append([e,loss_total])# 로스 (loss)값 추이 확인
import pandas as pd
df=pd.DataFrame(loss_track,columns=['E','L'])
import seaborn as sns
import matplotlib.pyplot as plt
sns.scatterplot(data=df,x='E',y='L')
plt.yscale('log')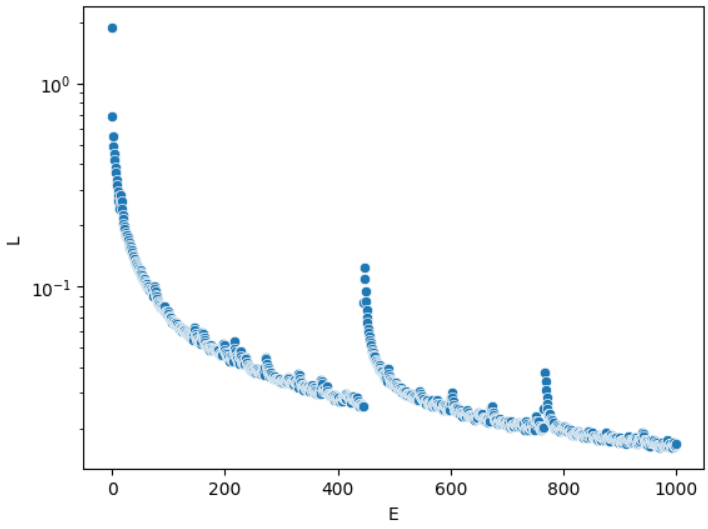
# 메모리 모듈
from torch.nn import functional as F
class memory(nn.Module):
def __init__(self,memory_size,feature_size):
'''
memory_size : 메모리의 크기 (M)를 얼마로 설정하는지 결정한다.
feature_size : 인코더를 통과한 latent vector의 크기와 동일한 특징 크기 (F)로 설정해야한다.
이를 통해 메모리의 크기는 M-by-F 행렬이 된다.
'''
super(memory,self).__init__()
self.memory=nn.parameter.Parameter(torch.randn(memory_size,feature_size), requires_grad=True) # M x F
self.softmax=nn.Softmax()
self.hard_shirinkage=5/memory_size
# hard_shirinkage는 복원 시에 과적합이 발생하지 않도록 softmax 통과 후의 확률값 중
# 기준치를 미달한 것들을 0으로 만들기 위해 만든 것이다.
# 원본 저자들은 메모리 사이즈가 N이면 1/N ~ 3/N 정도가 적당하다고 했지만 꼭 그러지는 아니었다.
self.relu=nn.ReLU()
def forward(self,_input):
similarity=F.linear(_input,self.memory) # encoded x memory = (1 x F) x (F x M)
# 코사인 유사도는 엄밀하게 따지면 두 가지 벡터의 크기로 나눠줘야하지만 원본저자들도 안해서
# 나도 안했다. 엄밀히 따지면, 벡터의 크기를 1로 제한하는 기능이 있어야 하지만 여기서는 넘어간다.
prob=self.softmax(similarity)
# 소프트 맥스를 통과하면 확률값이 나온다.
diff=prob-self.hard_shirinkage
# diff는 ReLU함수를 통과하기 전에 기준치를 통과하는지 판단하기 위해 만들었다.
prob=F.normalize(self.relu(diff)*prob/(diff.abs()+1e-12),p=1,dim=1)
# hard-shirinkage 후 다시 새로운 확률값으로 만들어준다.
memorized_image=F.linear(prob,self.memory.T) # prob x memory = (1 x M) x (M x F)
# 확률값을 메모리에 곱해서 정상 latent vector로부터 이미지를 복구한다.
return memorized_image,prob
# 기억한 이미지와 유사도 확률값을 내보낸다.
그렇다면 훈련 전에는 무작위 행렬로 되어있는 벡터에서 디코딩 시에 무엇이 나오는지 보자
M=memory(memory_size=100,feature_size=64)
rM=D(M.memory)
grid=(1,8);loc=[0,0]
plt.figure(figsize=(20,4))
n_rows=2;n=0
for i in range(len(rM)):
if i%(grid[1])==0 and i!=0:
n+=1
plt.show()
loc[1]=0
plt.figure(figsize=(20,4))
if n_rows==n:
break
i1=rM[i].reshape(28,28).detach().cpu().numpy()
plt.subplot2grid(grid,loc=loc)
plt.imshow(i1)
loc[1]+=1
plt.show()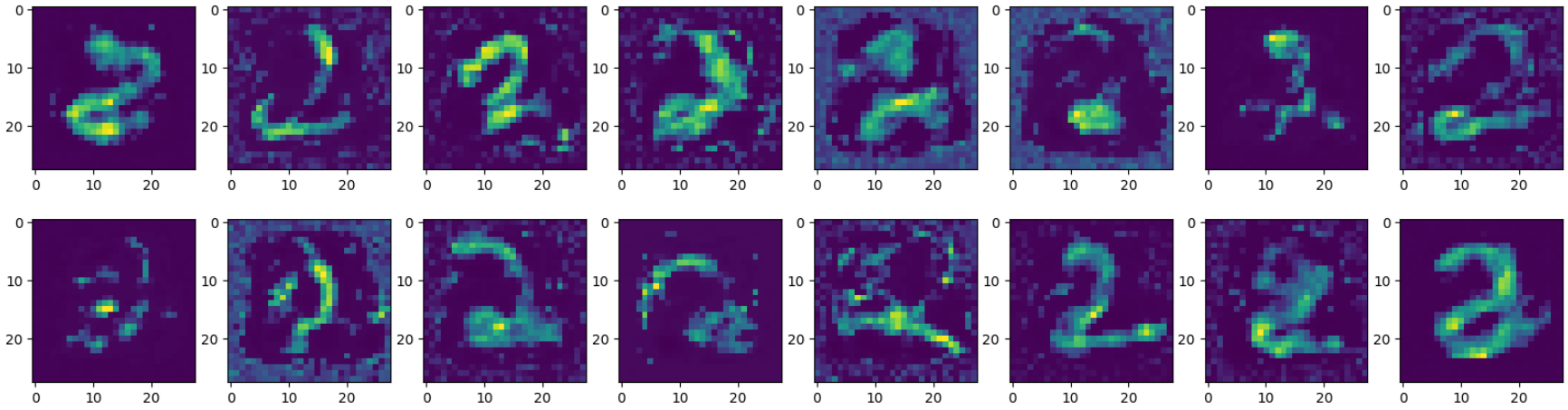
디코더로 인해 2와 유사한 모습을 띠고 있지만 명확하지는 않다.
def calculate_entropy(x,eps=1e-10):
# x=similar[2]
x1=x+eps
entropy=-torch.log(x1)*x1
return entropy.sum(axis=1)
# 메모리 학습 시작
loss_track_M=[]
E.eval();D.eval();M.train()
from tqdm import tqdm
E.to(f'cuda:{device}');D.to(f'cuda:{device}');M.to(f'cuda:{device}')
for e in tqdm(range(epoch)):
train = torch.utils.data.DataLoader(pdata['train-dataset']['Normal'], batch_size=batch_size,shuffle=True,drop_last=True)
loss_total=0
for t in train:
t=t.to(f'cuda:{device}').view(batch_size,-1)
encoded=E(t)
most_similar=M(encoded)
rE=D(encoded)
rM=D(most_similar[0])
loss1=criterion(rE,rM) # D(E(x))와 D(M(E(x)))의 재구축 오차값을 산출한다.
loss2=calculate_entropy(x=most_similar[1],eps=1e-10).sum()/len(t) # 얼만큼 확신을 갖는지에 대한 cross entropy
loss_fin=loss1+0.0002*loss2.item()
optim_M.zero_grad()
loss_fin.backward()
optim_M.step()
loss_total+=loss_fin.item()
loss_track_M.append([e,loss_total])# 메모리 손실함수 기록
import pandas as pd
df_M=pd.DataFrame(loss_track_M,columns=['E','L'])
import seaborn as sns
import matplotlib.pyplot as plt
sns.scatterplot(data=df_M,x='E',y='L')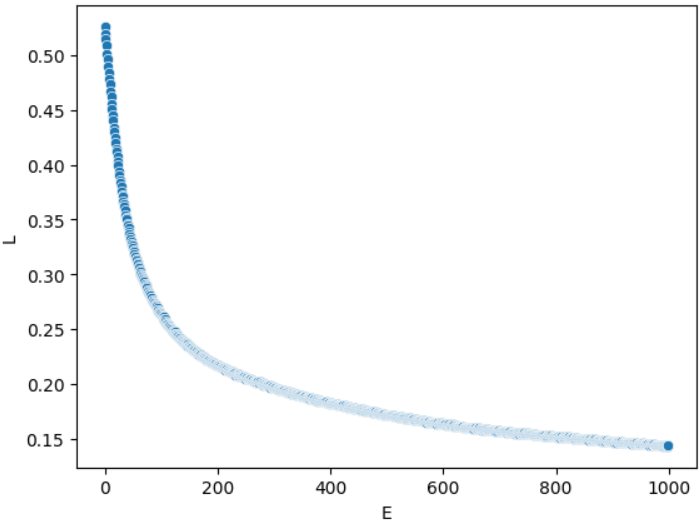
# 학습 완료 후 메모리의 잠재 벡터로 부터 디코딩된 이미지들
rM=D(M.memory)
grid=(1,8);loc=[0,0]
plt.figure(figsize=(20,4))
n_rows=3;n=0
for i in range(len(rM)):
if i%(grid[1])==0 and i!=0:
n+=1
plt.show()
loc[1]=0
plt.figure(figsize=(20,4))
if n_rows==n:
break
i1=rM[i].reshape(28,28).detach().cpu().numpy()
plt.subplot2grid(grid,loc=loc)
plt.imshow(i1)
loc[1]+=1
plt.show()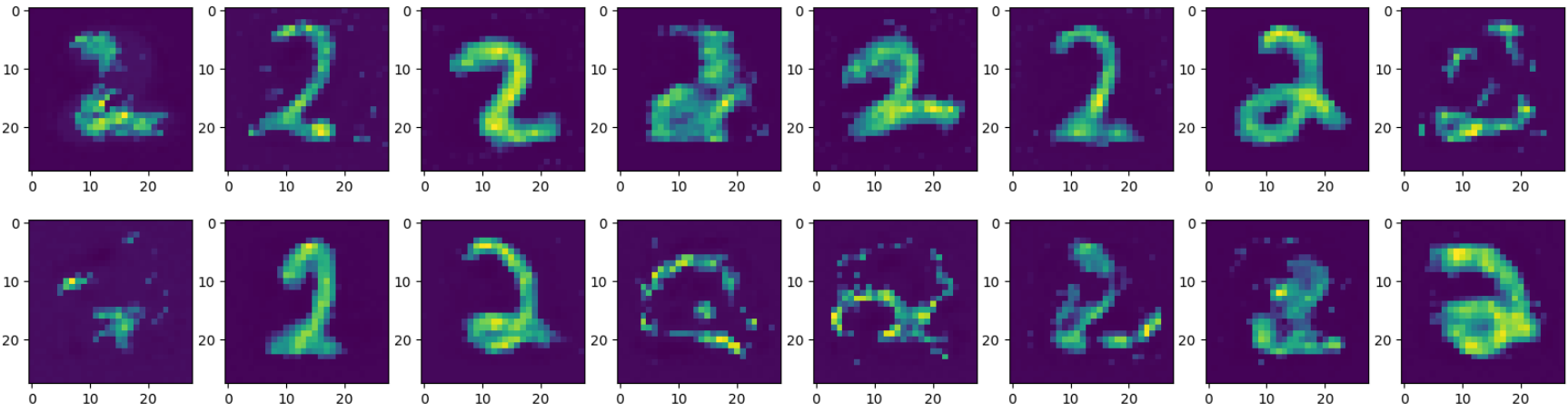

훈련 전 후의 이미지들을 비교하면 모두 그런 것은 아니지만 훈련 후에 보다 명확한 이미지가 된 것을 볼 수 있다.
잠재 공간에서의 2의 이미지는 몇 번 테스트 해봤을 때 메모리 사이즈 (M)이 작을 수록 명확한 2로 보였다.
# 이상치 점수 계산
def calculate_anomality_score_from_cAE(x=pdata['train-dataset']):
# 전통적인 오토인코더로 계산.
result=[]
for key in ['Normal','Anormal']:
# Reshaping
x1=x[key]
x2=x1.view(len(x1),-1).to(f'cuda:{device}')
# Calculate Reconstruction-error
fake_img=D(E(x2))
error=((x2-fake_img)**2).sum(axis=1).detach().cpu().numpy().flatten()
df=pd.DataFrame([])
df['label']=[key]*len(error)
df['error']=error
result.append(df)
result=pd.concat(result,axis=0)
return result
pdata['anomaly-from-cAE']=calculate_anomality_score_from_cAE(x=pdata['train-dataset'])def calculate_anomality_score_from_mAE(x=pdata['train-dataset']):
# 메모리 기반 오토인코더로 진행
result=[]
for key in ['Normal','Anormal']:
# Reshaping
x1=x[key]
x2=x1.view(len(x1),-1).to(f'cuda:{device}')
# Calculate Reconstruction-error
encoded=E(x2)
try:
most_similar=M(encoded)[0]
except:
most_similar=M(encoded.reshape(1,5842,64))[0]
fake_img=D(most_similar)
fake_img2=D(encoded)
error=((x2-fake_img)**2).sum(axis=1).detach().cpu().numpy().flatten()
error2=((x2-fake_img2)**2).sum(axis=1).detach().cpu().numpy().flatten()
# 여기서 전통적인 오토인코더와 메모리 모듈의 재구축 오차값을 모두 더한다.
# 원본 논문에서는 이러지 않았지만 내 경우에는 이렇게 할 때 성능이 좀 더 나았다.
df=pd.DataFrame([])
error_total=error+error2
df['label']=[key]*len(error_total)
df['error']=error_total
result.append(df)
result=pd.concat(result,axis=0)
return result
pdata['anomaly-from-mAE']=calculate_anomality_score_from_mAE(x=pdata['train-dataset'])from sklearn.metrics import roc_curve,auc
def evaluation(pdata):
plt.plot([0,1],[0,1],linestyle='dotted',color='grey')
for key in ['anomaly-from-cAE','anomaly-from-mAE']:
k1=pdata[key]
fpr,tpr,_=roc_curve(y_true=k1['label']=='Anormal',y_score=k1['error'].values)
aucv=auc(fpr,tpr)
label_name=key.split('-')[-1]
plt.plot(fpr,tpr,label=f'{label_name} ({aucv:.5f})')
plt.legend()
plt.show()
evaluation(pdata)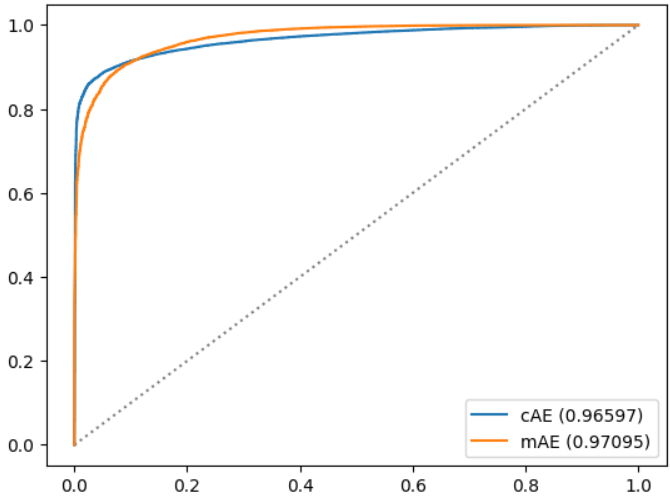
pdata['anomaly-from-cAE']=calculate_anomality_score_from_cAE(x=pdata['test-dataset'])
pdata['anomaly-from-mAE']=calculate_anomality_score_from_mAE(x=pdata['test-dataset'])
evaluation(pdata)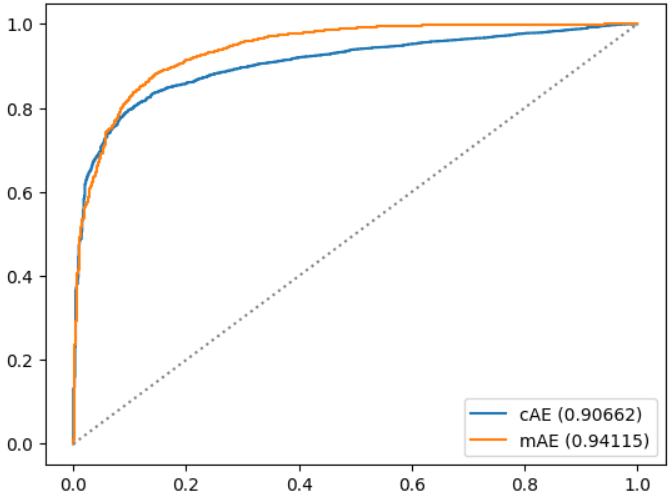
3. 결론
메모리 지도 오토인코더는 훈련 데이터셋에서는 더 낫다고 하긴 어려웠지만 새로운 데이터셋에서는 보다 나은 결과를 제공해줬다. 하지만, 반드시 이런 것은 아니며 메모리 사이즈의 크기의 영향이 꽤 컸으며 hard_shirinkage의 값도 민감하게 반응했다.
출처 :
Memorizing Normality to Detect Anomaly: Memory-augmented Deep Autoencoder for Unsupervised Anomaly Detection