728x90
반응형
1. 개요
이진 변수 (binary variables)는 2가지의 가능한 값들 중 하나를 정량화하는 것에 쓰일 수 있다. 하지만, 우리는 자주 K개의 상호적으로 겹치지 않는 상태들에 대해 마주할 수 있다. 다양한 방식으로 이를 서술할 수 있지만 편의상 1-of-K 개념 (1-of-K scheme)으로 살펴보려한다.
2. 내용
- 이 개념에서는 변수는 K차원의 벡터 x에 의해 표현되며 벡터 x의 원소 x_k는 1이고 나머지 원소들은 0이다. 예를들어 K=6개의 상태로 표현하면서 x_3=1이라면 벡터 x는 수식 2.25와 같이 표현된다.

- 여기서 벡터 x의 원소들의 합은 1을 만족한다. 만일 우리가 u_k라는 파라미터로 x_k=1의 확률로 나타내면 벡터 x의 분포는 수식 2.26과 같이 나타난다. 여기서 u_k의 합은 1이며 0보다 크다. 수식 2.26은 베르누이 분포를 2개 이상의 결과들에 대해 일반화한 형태로 생각될 수 있다.
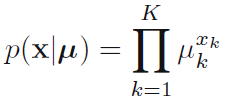

- 분포는 수식 2.27과 같이 표준화 될 수 있으며 이는 수식 2.28로 이어진다.


- 이제 N={x_1,....,x_N}개의 관측값으로 이루어진 데이터세 D를 고려하자. 이것에 상응하는 가능도 함수는 수식 2.29로 나타낼 수 있다.

- 위의 수식에서 가능도 함수는 N개의 데이터포인트에 의존적인걸 확인할 수 있다. 이 N은 K로 정량한다.
수식 2.30은 x_k=1인 관측값들의 숫자를 나타낸다. 이것들을 이 분포에 대한 충분한 통계치 (sufficient statistics)라고 부른다.

- u에대한 최대가능도 함수를 찾기 위해, u_k에 대해 ln[p(D|u)]를 최대화시킬 필요가 있다. 이것의 제한조건은 u_k의 총합이 1이 되야하는 것이다. 이것은 라그랑주 승수 (Lagrange multiplier) lambda를 사용하면서 수식 2.31을 최대화 시키면 된다.

- 2.31의 u_k에 대한 미분값을 0으로 설정하면 수식 2.32를 얻을 수 있다.

- 라그랑주 승수 lambda값은 수식 2.32에 대해 u_k의 총합은 1이라는 조건을 넣어서 구할 수 있다. 이것은 lambda = -N의 값을 구할 수 있게 한다. 따라서, 최대 가능도 해법은 수식 2.33과 같이 나타난다.
이는 x_k=1이란 값에 대한 N개의 관측값에서의 비율이다.

- 파라미터 u와 N개의 관측값들의 숫자에 대한 조건에 대해 우리는 정량값들 m_1,....,m_k의 결합 분포를 고려할 수 있다. 수식 2.29에서 수식 2.34를 유도할 수 있다. 이것이 다항 분포 (mutinomial distribution)으로 알려진 수식이다.

- 표준화 상수 (normalization coefficient)는 N개의 관측값들을 m_1,....,m_k의 크기의 K그룹으로 분할하는 숫자들이다. 이는 수식 2.35로 주어진다.

- 변수 m_k는 수식 2.36의 제한사항이 있다.

728x90
반응형
'DeepLearning > Pattern recognition and Machine learning' 카테고리의 다른 글
| [PRML] 2.2.1 The Dirichlet distribution (디리클레 분포) (0) | 2024.03.04 |
|---|---|
| [PRML] 2.1.1 The beta distribution (베타 분포) (0) | 2024.02.06 |
| [PRML] 2.1. Binary variables (이진 변수들) (0) | 2024.02.01 |
| [PRML] 2. Probability distributions (확률 분포들) (0) | 2024.01.26 |
| [PRML] 1.6.1 Relative entropy and mutual information (상대 엔트로피와 상호 의존 정보) (0) | 2024.01.23 |


