728x90
반응형
1. 개요
- 챕터 2에서 확률 분포들의 중요한 특징들을 서술하겠지만 여기서는 표준 혹은 가우시안 분포라 불리는 확률 분포를 소개함. 가우시안 분포는 책 전반에 걸쳐서 많이 사용됨.
2. 내용
- 가우시안 분포는 실수값인 단일 변수 x에 대해 수식 1.46과 같이 정의됨.
이것은 평균값 u (뮤)와 분산 sigma**2으로 조절된다. sigma는 표준 편차 (standard deviation)라고 불림.
분산의 역수(1/sigma**2)는 정밀도 (precision)이라고 불림.

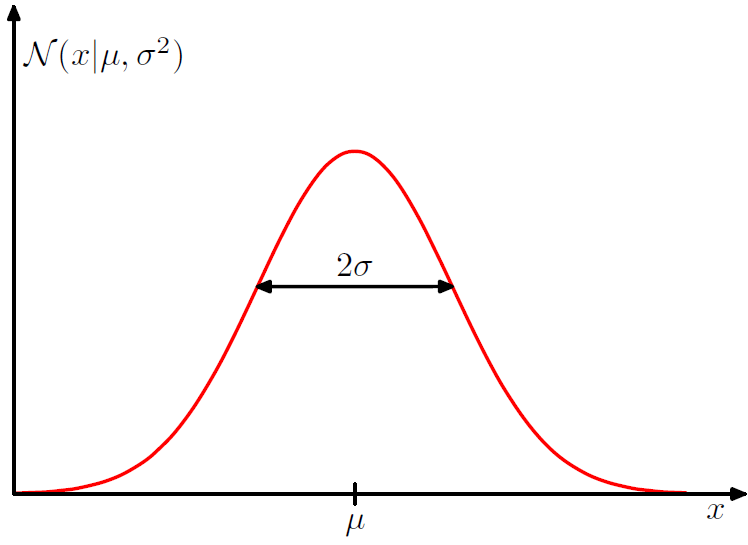
- 가우시안 분포는 1.47을 만족한다. 즉, 항상 양수라는 것이다.

- 가우시안 분포를 표준화 (normalized) 하면 수식 1.48과 같이 표현된다. 따라서, 수식 1.46은 유효한 확률 밀도에 필요한 2가지 조건을 만족한다.

- 가우스 분포 아래 x에대한 기대값들은 수식 1.49와 같이 표현됨.
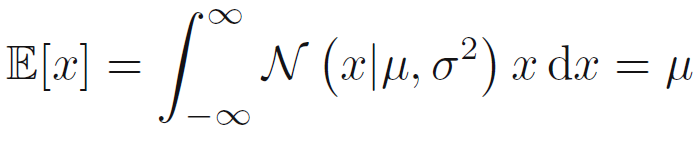
- x제곱의 기대값들은 수식 1.50과 같이 표현됨.
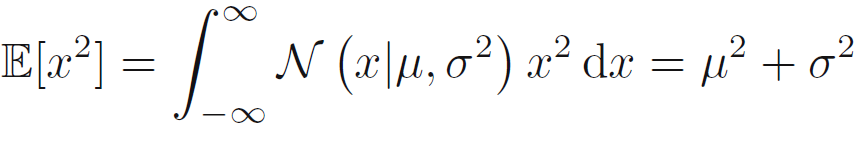
- 가우시안 분포의 분산은 수식 1.49와 수식 1.50을 통해 수식 1.51과 같이 표현됨.

- 연속적인 값들로 이루어진 D 차원의 벡터 x에 대한 가우시안 분포는 수식 1.52와 같이 규정된다.
u는 D 차원 벡터의 평균값이고 DxD 행렬인 시그마 (sigma)는 공분산이며 |sigma|는 시그마의 행렬식 (determinant)를 의미한다. 다변량 가우시안 분포는 챕터 2.3에서 좀 더 자세하게 다룬다.
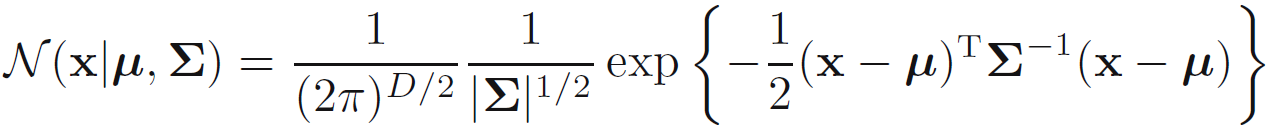
- 이제 관측값들로 이루어진 데이터셋 X=(x1,.....,xN)T이 있다고 하자. 여기서 N은 관측치 수를 의미하고 x는 스칼라값이다. 여기서 X로 볼드체로 표기했는데 개별적인 관측치는 벡터값으로 이루어진 데이터 셋 X와 다르게 표현하기 위함임. 같은 분포에서 독립적으로 데이터 포인트들이 추출됐다면 이를 independent and identically distributed로 표현하며 줄여서 i.i.d로 말함.
2개의 독립적인 사건들의 결합확률은 각 사건의 합확률 (marginal probability)의 곱이므로, X 데이터셋의 확률을 주어진 평균값과 분산을 통해 수식 1.53과 같이 표현가능함.
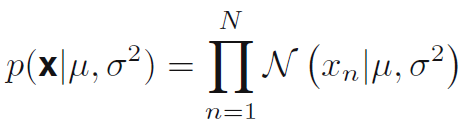
- 이것을 평균 (mu)와 분산에 대한 함수로 볼 때, 이것은 가우시안 분포에 대한 가능도 함수 (liklihood function)이며 그림 1.14처럼 해석될 수 있다.
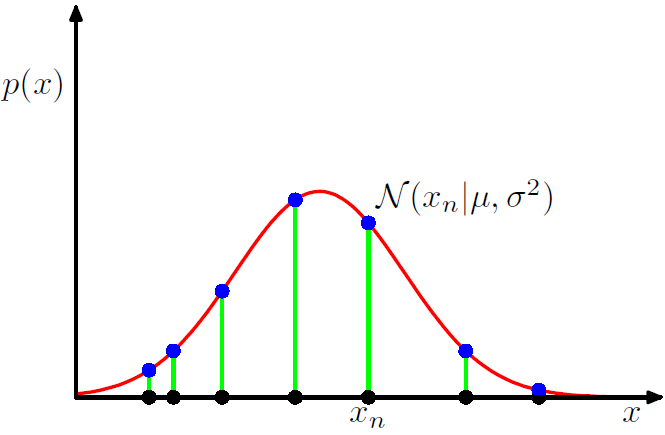
- 관측된 데이터셋을 활용해서 어떤 확률분포를 따르는 파라미터들을 결정하는 일반적인 기준은 가능도함수를 최대화 하는 파라미터들을 찾는 것이다. 확률이론을 생각할 때, 이것은 주어진 데이터셋에 대해 파라미터들의 확률을 최대화 하는 것이 맞는 것으로 보여 이상하게 생각될 수 있다. 하지만, 2가지 방식들은 서로 관련되어 있으며 이것은 커브 피팅 (curve fitting)에서 다시 논의한다. 일단은 알지 못하는 파라미터 평균과 분산을 결정하는 과정을 가능도 함수를 최대화 시키는 것을 통해 보이고자 한다.
- 실용적으로 가능도 함수의 최대화는 로그 가능도 함수 (log of the liklihood function)을 통해 하는 것이 쉽다. 이유는 로그함수는 단조증가 (monotonically increasing)하기 때문에 로그를 씌우기 전의 함수를 최대화 하는 것과 동일하기 때문이다. 또한, 컴퓨터의 underflow 현상을 회피하기에 용이하다.
여기서, 단조함수를 쉽게 설명설명하면 주어진 순서를 보존하는 함수를 의미한다. x>0일 때 y=x나 y=log(x)나 x값이 증가하면 y값도 증가한다. 이러한 것을 단조함수라고 한다. - 수식 1.46과 1.53을 로그 가능도 함수로 변환하면 수식 1.54 수식으로 나타난다.

- 평균 (u)에 대해 최대화할 때 최대 가능도 해 (maximum likelihood solution)은 수식 1.55로 나온다.
이것은 샘플들의 평균 (sample mean)이다. 다시말해, 관측된 값들의 평균이다.
이와 유사하게, 수식 1.54를 분산에 대해 최대화 할 경우 수식 1.56으로 나온다. 이것은 샘플 평균에 대한 샘플 분산값이다. 여기서 주의할 점은 우리는 현재 수식 1.54는 평균과 분산을 동시에 최대화하고 있다. 하지만, 평균과 분산의 가우시안 분포 해가 서로 분리되어 있으므로, 수식 1.55를 수행한 후에 해당값을 가지고 수식 1.56을 수행할 수 있다.
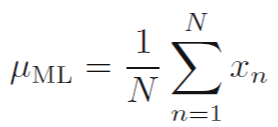

- 나중에 최대가능도접근법 (maximum likelihood approach)의 중대한 한계를 다룰 것이다. 특히, 이 방식은 분포에 대한 분산을 시스템적으로 과소평가하게 된다. 이 현상은 편향 (bias)라 불리며 다항함수 피팅 시에 보게되면 과적합 (over-fitting) 문제와 관련되어 있다.
- 최대 가능도 해인 u_ml과 v_ml들은 데이터셋의 값들 {x1, ...., xN} 에 대한 함수이다. 이러한 양의 기대값을 고려해 봅시다. 이 값들은 자체적으로 μ와 σ2 매개변수를 가진 가우시안 분포에서 나온 데이터 집합 값입니다. 이것들은 수식 1.57과 1.58로 표현됩니다. 이를 통해 알 수 있는 것은 보통 최대 가능도 예측 (maximum likelhood estimate)은 정확한 평균을 얻을 수 있지만 실제 분산에 대해서는 (N-1)/N만큼 과소 평가하게 됩니다.
이것의 증명과정은 베셀교정 확인바람.

- 수식 1.58로부터 수식 1.59의 분산 파라미터 (variance parameter) 추정치는 편향되지 않음을 알 수 있습니다.
(마찬가지로 베셀교정 확인바람)
수식에서 알 수 있듯이 N이 커지면 커질수록 최대 가능도 해의 편향의 교정은 덜 중요해지며 N이 무한대가 되면 관측값들이 생성된 분포의 분산값과 동일해진다.

- 실제로, N이 매우 작은 경우를 제외하고 이 편향은 심각한 문제를 일으키진 않는다. 하지만, 이 책에서는 많은 변수들이 있는 복잡한 모델들을 다룰 것이고 이러한 최대 가능도와 관련된 편향 문제가 심각해지는 것을 확인할 것이다. 실제로, 이러한 편향은 과적합 문제의 근본적인 원인이다.
728x90
반응형
'DeepLearning > Pattern recognition and Machine learning' 카테고리의 다른 글
| [PRML] 1.2.6 Bayesian curve fitting (베이지안 곡선 피팅) (0) | 2023.12.26 |
|---|---|
| [PRML] 1.2.5 Curve fitting re-visited (0) | 2023.12.15 |
| [PRML] 1.2.3 Bayesian probabilities (베이지안 확률들) (0) | 2023.11.07 |
| [PRML] 1.2.2 Expectations and covariances (기대값과 공분산) (0) | 2023.11.06 |
| [PRML] 1.2.1 Probability densities (확률 밀도) (0) | 2023.11.03 |



