728x90
반응형
1. 개요
앞선 내용들에서 다항 커브 피팅 (polynomical curve fitting)이 오차 최소화 (error minimization)으로 표현되는지 확인함. 이제 커브 피팅 예제로 돌아가서 확률적 관점에서 다루고자함. 이를 통해 오차 함수 (error function)과 정규화 (regularization)에 대한 영감을 얻고 완전한 베이지안 방법론 (bayesian technique)에 다가가고자 한다.
2. 내용
- 커브피팅 문제는 새로운 변수 x에 대해 표적 변수 t를 예측하는 것으로 N개의 입력값 벡터 x로 이루어진 훈련데이터를 통해 하는 것이다. 표전 값에 대한 불분명함 (uncertainty)를 확률 분포를 통해 표현할 수 있다. 이 목적을 위해 주어진 x에 대해 t는 다항함수의 y(x,w)라는 값과 동일한 평균값을 갖는 분포를 따른다고 하자. 이는 수식 1.60으로 표현된다.
여기서 정밀도 파라미터 beta는 분포의 분산의 역수에 대응한다 (beta corresponding to the inverse variance of the distribution). 이는 그림 1.16으로 표현된다.


- 이제 알지 못하는 파라미터 w와 beta를 최대 가능도를 통해 결정하기 위해 훈련 데이터 {x,t}를 사용하겠다. 이 때, 데이터들은 독립적으로 수식 1.60의 분포에서 추출됐다고 가정하면 수식 1.61과 같이 가능도 함수가 정의된다.

- 로그 가능도 함수를 최대화 시키는 것이 효율적이므로 이를 로그 가능도 함수 (log likelihood function)으로 나타내면 수식 1.62와 같이 된다. 수식 1.61에서 수식 1.62로 넘어가는 과정에서 N(t_n|y(x_n,w))가 {y(x_n,w)-tn}**2으로 변하는 것은 수식 1.46을 보면 된다. 평균값이 y(x_n,w)일 때 정답값인 t_n이 나타날 확률을 나타낸 것이라 보면 된다.
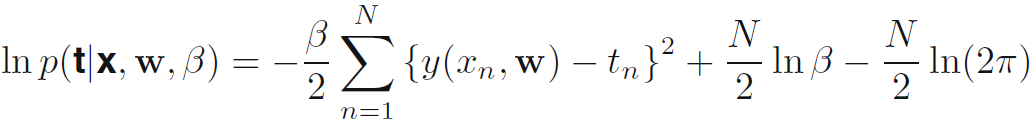

- w_ml로 표기되는 다항함수의 계수들에 대한 최대가능도 해의 결정을 우선 생각해보자. 이것들은 1.62를 w에 대해 최대화하면 결정된다. 이 목적일 때, 수식 1.62의 우변에서 마지막 2개 요소들을 생략할 수 있다. 이유는 이들은 w에 대해 독립적이기 때문이다. 또한, 이 해를 계산할 때, 양의 상수는 별 영향을 안주는 것을 알 수 있으므로 beta/2를 1/2로 바꿀 수 있다 (beta는 정밀도이므로 음의 값이 아니라 양의 값이다.). 마지막으로, 로그 가능도를 최대화하는 것은 음수 로그 가능도를 최소화 하는 것과 동일하다 따라서, w를 결정하는 것에대해 우리가 다루고 있는 부분에서는, 가능도를 최대화 하는 것은 sum-of-squares error function (수식 1.2)를 최소화 하는 것과 동일하다. 따라서, 가우시안 노이즈 분포의 가정 아래에서 가능도를 최대화 하는 것의 결론에서 sum-of-squares error function이 나온 것이다.
- 정밀도 파라미터 베타를 최대 가능도를 활용하여 결정하는 것도 가능하다. 수식 1.62를 beta에 대해 최대화 하면 수식 1.63과 같이 나타난다.

- 이렇게 결정된 파라미터 w와 beta를 가지고 x의 새로운 값을 예측할 수 있다. 이것은 일종의 확률적 모델 (probablistic model)이기 때문에, t에 대한 확률 분포를 주는 예측 분포 (predictive distribution)로 표현될 수 있다. 그리고, 수식 1.60에서 최대가능도 파라미터를 채워넣어서 얻을 수 있다. 이는 수식 1.64로 표현된다.


- 베이지안 방법론에 좀 더 다가가기 위해 다항함수 계수 w에 대한 사전확률을 도입해보자. 간결함을 위해 다음과 같은 가우시안 형태의 분포를 고려하겠음 (수식 1.65). 여기서 alpha는 분포의 정밀도를 의미하며 M+1은 M차항의 다항함수에 대한 벡터 w의 모든 원소의 수를 의미함. alpha와 같이 모델 파라미터들의 분포를 조절하는 변수를 하이퍼파라미터 (hyperparameter)라고 부름.

- 베이지안 정리를 이용하면 w에대한 사후확률은 가능도함수와 사전확률 분포의 곱셈에 비례함. (수식 1.66)
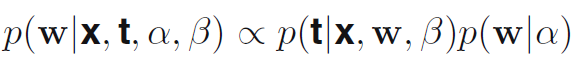
- 이제 주어진 데이터에 대해 w의 가장 가능성있는 값을 찾음으로서 w를 결정할 수 있음. 다시 말해, 사후 확률을 최대화 한다는 것임. 이것을 최대 사후 확률 (maximum posterior) 또는 줄여서 MAP라고 부름. 수식 1.66을 음의 로그를 취하고 수식 1.62와 1.65를 합치면 사후확률의 최대화는 수식 1.67을 최소화 함으로서 얻을 수 있음.

- 따라서, 사후확률 분포 (posterior distribution)을 최대화 한다는 것은 정규화 파라미터 lambda = alpha/beta로 주어진 sum-of-squares error function (수식 1.4)을 최소화 한다는 것과 동일하다는 것을 알 수 있다.
728x90
반응형
'DeepLearning > Pattern recognition and Machine learning' 카테고리의 다른 글
| [PRML] 1.3 Model Selection (모델 선택) (0) | 2023.12.28 |
|---|---|
| [PRML] 1.2.6 Bayesian curve fitting (베이지안 곡선 피팅) (0) | 2023.12.26 |
| [PRML] 1.2.4 The Gaussian distribution (가우시안 분포) (0) | 2023.11.08 |
| [PRML] 1.2.3 Bayesian probabilities (베이지안 확률들) (0) | 2023.11.07 |
| [PRML] 1.2.2 Expectations and covariances (기대값과 공분산) (0) | 2023.11.06 |



