[PRML] 1.5.1 Minimizing the misclassification rate (잘못된 분류율 최소화하기)

1. 개요

 우리의 목적이 간단히 잘못된 분류를 최소화 하는 것이라고 가정해봅시다. 이를 위해, 우리는 x에 대해 어떤 클래스로 지정할 때 규칙이 필요합니다. 이 규칙은 결정 영역 (decision regions)이라 불리는 입력 공간 Rk를 각 클래스 별로 나눌 것입니다. 이를 통해, Rk내의 모든 데이터 포인트들은 클래스 Ck에 속하게 됩니다. 결정 영역 사이의 경계선들은 결정 경계 (decision boundaries) 또는 결정면 (decision surfaces)라 불립니다.
 알아둘 점은 결정영역은 꼭 인접할 필요는 없습니다. 이것들은 비결합 영역 (disjoint regions)일 수도 있습니다. 결정 경계와 결정 영역에 대해서는 다음 챕터들에서도 계속 다루겠습니다.

 

2. 내용

• 최적의 결정규칙을 찾기 위해, 앞의 암 진단문제와 같은 2가지 클래스로 이루어진 것들을 고려해보겠음.
  C1에 속하는 입력변수가 C2에 잘못 배정되거나 그 반대는 실수라고 한다. 이러한 실수 확률은 수식 1.78과 같다.

수식 1.78

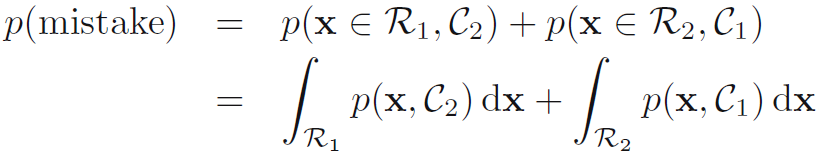
• 분명히 p(mistake)를 최소화하기 위해서는 수식 1.78에서 낮은 값이 나오도록 x를 배정해야한다. 따라서 만일 주어진 x에 대해 p(x,C1) > p(x,C2)라면 우리는 x를 C1에 배정해야할 것이다. 확률 곱셈 법칙에 의해, p(x,Ck) = p(Ck|x)p(x)이다. p(x)는 양변에 모두 공통되므로 사후확률 p(Ck|x)가 최대화 되는 지점에서 p(mistake)가 최소화 된다고 말할 수 있다. 이것은 단일 변수 x일 때에 대해 그림 1.24로 나타난다.

그림 1.24. 2가지 클래스에 대한 결합 분포 p(x,Ck). 결정 경계는 x=x_het이다. x_het을 이동할 때 파란색과 초록색 영역은 그대로지만 빨간색 영역은 변하게 된다. x_het에 대한 최적의 선택은 p(x,C1)과 p(x,C2)가 교차하는 지점이며 이 지점은 x0=x_het일 때이다. 이유는 빨간색 영역이 사라지기 때문이다.

• 보다 일반적인 상황인 K개의 클래스에 대해서는 올바르게 선정할 확률을 최대화 하는 것이 보다 쉬우며 이는 수식 1.79로 나타난다. 아래 수식이 최대화 되는 것은 각 x가 올바르게 선정될 확률인 p(x,Ck)가 최대화 되는 영역 Rk를 잡을 때이다. 다시, 곱셈 규칙을 이용하여 p(x,Ck) = p(Ck|x)p(x)이며 p(x)는 모든 것 (all terms)에 공통되므로 각 x는 사후확률 p(Ck|x)가 최대화 되는 클래스에 지정해야 맞다.

수식 1.79