728x90
반응형
1. 개요
최소 제곱 (least squares)을 활용한 다항함수 커브 피팅 문제 예제를 통해, 가장 좋은 일반화 (the best generalization)을 줄 수 있는 적절한 다항함수의 차수 (optimal order of polynomial)가 있다는 것을 확인했다. 해당 차수는 모델의 파라미터를 조절하고 모델의 복잡도를 조절한다.
정규화된 최소 제곱 (regularized least squares)에서 정규화 상수 lambda 또한 모델의 복잡도를 조절한다. 신경망과 같은 좀 더 복잡한 모델들은 더 많은 파라미터가 모델의 복잡도에 관여할 수 있다. 이러한 상황에서, 모델의 복잡도를 조절하는 파라미터의 값들을 연구자들은 정해야 하며 이는 새로운 데이터에 대한 최상의 예측력을 달성하기 위함이다. 추가적으로, 적절한 모델의 복잡도를 찾는 것 뿐만 아니라, 특정한 상황에서 최고의 모델을 찾기 위해 여러 종류의 모델을 고려해야할 수 있다.
2. 내용
- 최대 가능도 접근법에서 나왔듯이 훈련데이터에대한 성능은 과적합 우려가 있다. 그래서, 일반적인 예측력을 평가할 때 좋은 것은 아니다. 만일 데이터가 충분히 많다면, 활용 가능한 데이터 중 일부를 훈련하고 복잡도를 조절하고 평가하는데 사용할 수 있다. 이러한 데이터셋을 검증셋 (validation set)이라고 부르며 해당 데이터에서 가장 좋은 성능을 보이는 것을 선택하곤 한다.
- 하지만, 만일 모델 설계가 제한된 데이터 셋으로 많이 반복된다면, 검증 셋에 대해서도 과적합이 발생할 수 있다. 따라서, 세번 째 데이터셋인 테스트 셋 (test set)을 분리하여 모델을 평가할 때만 사용해야할 수 있다.
- 보통 훈련, 검증, 테스트 셋을 구비하기에 어려운 경우가 많다. 검증 셋이 작을 경우 예측력을 저하시키는 요인이 될 수 있다. 이러한 딜레마를 해결하는 방법 중 하나는 교차검증 (cross-validation)으로 그림 1.18에 나와있다. 이 방식은 전체 데이터셋에서 (S-1)/S 만큼의 데이터는 훈련에 사용하고 나머지 1/S는 검증에 사용해 성능 평가에 사용할 수 있다. 데이터가 지극히 적은 경우에는 S의 숫자를 N까지 늘려서 할 수도 있는데 이를 leave-one-out 기법이라 한다.
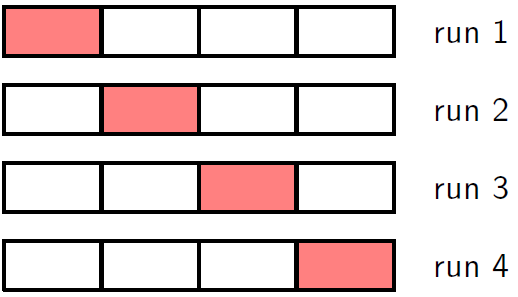
- 교차검증의 단점은 S에 따라서 훈련의 횟수가 증가한다는 것이며 컴퓨터 비용적으로 비싼 모델에 대해 문제를 발생시킨다. 또한, 단일 모델에 대해 여러가지 복잡한 파라미터를 평가해야할 때 역시 문제가 될 수 있다. 이 경우, 파라미터의 종류에 따라 시간 소모가 지수적으로 증가할 수 있다. 따라서, 훈련데이터만으로 다양한 종류의 파라미터와 모델을 한 번에 평가할 수 있어야 한다. 동시에, 과적합 문제도 해결해야한다.
- 이를 위해 다양한 정보기준 (information criteria)가 최대 가능도의 편향 (bias of maximum likelihood)을 교정하고자 제안됐다. 이들은 복잡한 모델의 과적합에 대해 페널티를 부과함으로서 작동한다. 예를들어 Akaike information criterion (AIC)는 모델을 선택할 때 수식 1.73이 최대화 되는 경우를 고른다. p(D|Wml)은 가장 잘 피팅된 상황에서의 likelihood이며 M은 조정가능한 파라미터의 수이다. 이외에도 Bayesian information criterion (BIC)와 같은 것들이 있는데 이는 챕터 3.4와 4.4.1에서 다룬다. 위의 기준들은 모델의 변수들의 불확실성을 고려하지 않고 간단한 모델을 과하게 선호하는 경향이 있다.
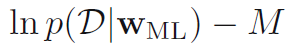
728x90
반응형
'DeepLearning > Pattern recognition and Machine learning' 카테고리의 다른 글
| [PRML] 1.5. Decision Theory (결정 이론) (0) | 2024.01.08 |
|---|---|
| [PRML] 1.4. The Curse of Dimensionality (차원의 저주) (0) | 2024.01.02 |
| [PRML] 1.2.6 Bayesian curve fitting (베이지안 곡선 피팅) (0) | 2023.12.26 |
| [PRML] 1.2.5 Curve fitting re-visited (0) | 2023.12.15 |
| [PRML] 1.2.4 The Gaussian distribution (가우시안 분포) (0) | 2023.11.08 |



