728x90
반응형
1. 개요
챕터 1에서 다양한 확률 이론과 결정 이론들의 개념들을 다뤄옴. 이번 챕터에서는 정보 이론 분야에서 몇 가지 추가적인 개념들을 도입하면서 마치겠음.
2. 내용
- 이산 무작위 변수 (discrete random variable) x에 대해 생각해봅시다. 그리고, 이 변수에 어떤 특정한 값을 확인했을 때 얼만큼 정보를 얻을 수 있을지 물어봅시다. 정보의 양 (amount of information)이란 x값을 배울 때의 놀라움의 정도 (degree of surprise)로 볼 수 있을 것입니다.
- 일어날 가능성이 매우 적은 사건 (a highly improbable event)가 일어난다면, 흔하게 일어나는 사건에 비해 더 많은 정보를 얻을 것입니다. 따라서, 확률 분포 p(x)에 정보량 (information content)는 의존하며 확률 p(x)에 단조 함수이면서 이를 반영하는 h(x)의 값을 찾고자 합니다.
- h(*)는 우리가 상관없는 두 가지 사건 x와 y가 있다고 가정하고 구해봅시다. 이 때 2가지 사건을 봐서 얻게되는 정보량은 각각에서 들어오는 정보량의 합이 되야 합니다. 따라서 h(x,y) = h(x) + h(y)입니다.
상관없는 사건들은 통계적으로 독립적이므로 p(x,y) = p(x)p(y)입니다. 이러한 관계들로부터, h(x)는 p(x)의 로그로서 주어진다는 것을 쉽게 보일 수 있습니다. 따라서, 수식 1.92와 같이 표현할 수 있습니다. 여기서 음수 표시는 정보가 양수이거나 음수임을 보장해줍니다. 이 수식에 따르면, 높은 정보량은 낮은 사건 확률과 대응됨을 볼 수 있습니다.

- 이제 어느 송신자가 랜덤 변수들을 수신자에게 보낸다고 가정해봅시다. 이 과정을 통해 전달되는 평균적인 정보량은 수식 1.92를 고려하면 수식 1.93과 같이 표기됩니다. 이 중요한 양을 랜덤 변수 x의 엔트로피 (entropy) 라고 부릅니다. 여기서 p(x)=0에서는 H[x]값이 0이 됩니다.

- 이 수식에 따르면 비균등분포 (nonuniform distribution)이 균등분포보다 더 작은 엔트로피를 갖습니다. 이를 활용하면 정리가 안된 상태에 대한 엔트로피의 해석을 할 수 있게 됩니다.
- 지금 당장은 수신자에게 변수들의 상태의 정체를 전달한다고 가정하고 이야기를 진행하겠습니다. 이것을 (생략함) 3-bit 숫자로 할 수 있습니다. 그러나, 비균등 분포의 이점을 활용하여서 좀 더 많은 사건이 일어나는 것에 대해 짧은 코드를 배치하고 적게 일어나는 것에는 긴 코드를 주는 방식으로 작성할 수 있습니다. 이를 통해 좀 더 짧은 코드 길이를 얻길 원하면서요. 예를들어 이것은 상태들의 집합 {a,b,c,d,e,f,g,h}를 {0,10,110,1110,111100,111101,111110,111111}로 나타낼 수 있을 것입니다. 이렇게 하면 평균적인 코드의 길이는 2bits가 됩니다. (수식 a)
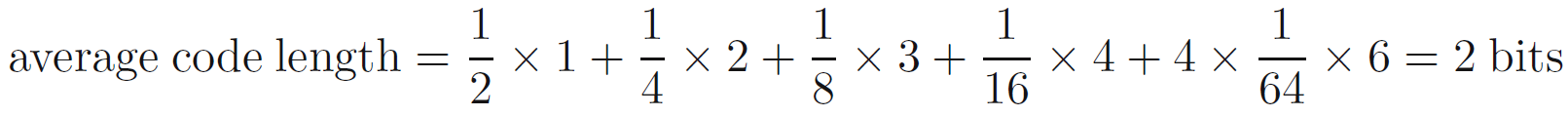
- 엔트로피와 최단 코드 길이 간의 이 관계는 일반적인 것입니다. 무잡음 코딩 이론 (noiseless coding theorem, Shannon, 1948)은 엔트로피가 확률 변수의 상태를 전송하는 데 필요한 비트 수의 하한이라고 명시하고 있습니다.
- 아래에서부터는 이 책에서 사용되는 많은 경우들에 쉽게 연동하기 위해 log2 대신에 자연로그 ln을 사용하겠습니다. 이 경우에 단위 (unit)은 bits 대신에 nats라고 부르게 됩니다.
- 지금까지 엔트로피의 개념을 무작위 변수의 상태를 정의하기 위한 평균적으로 필요한 정보량으로 소개했습니다. 사실은 이 개념은 물리학에서 훨씬 이전에 도입되어 있었습니다. 물리학에서는 이것을 열역학적인 평형상태의 개념으로 도입했고 이후 통계 역학 (statistical mechanics)의 발달을 통해 비질서의 양 (a measure of disorder)에 대한 해석으로 사용됩니다.
- 우리는 이러한 엔트로피의 다른 시각을 동일한 N개의 물체를 고려해서 이해할 수 있습니다. 해당 물체들은 일정한 집합 (a set of bins)로 나뉘어집니다. 이러한 방식으로 n_i 물체는 i번 째 bin에 속합니다. 이 물체들을 이러한 집합에 배정하는 여러가지 방법들을 생각해봅시다. 처음 물체를 선택하는 것에는 N개의 방법이 있습니다. 두 번 째에는 N-1개의 방법이 있고 이러한 방식으로 끝까지 가면 N! (factorial N, N x (N-1) x ..... x 2 x 1)의 방법이 있습니다. 여기서 i-th bin에는 n_i!의 물체 배열법이 있습니다. 여기서는 해당 집합 (bin)에서는 원소들의 배열을 고려하지 않기 때문에 이를 보정해주면 수식 1.94와 같이 N개의 물체를 집합들에 배정하는 경우의 수가 나옵니다. 이를 다양성/다중도 (multiplicity)라 합니다.
다중도 : 열역학계에서 특정한 거시상태 (macrostate)에 상응하는 미시상태 (microstate)들의 경우의 수
(the number of microstates corresponding to a particular macrostate of a thermodynamic system)

- 엔트로피는 적절한 상수로 크기를 조절하면 다음과 같이 다중성의 로그함수 형태 (수식 1.95)로 나타낼 수 있습니다.

- 이제 우리는 분수 n_i/N이 고정된 채로 N → ∞의 극한을 고려하고, 스털링의 근사 (수식 1.96)를 적용합니다.
그러면 수식 1.97이 나오게 됩니다. 여기서 sigma(ni) = N를 이용했습니다.
여기서 p_i = lim( N → ∞) [ni/N]은 i번 째 bin에 속할 확률입니다.


- 물리학 용어에서 bins들 안에서의 원소들의 특정한 배열은 미소상태 (microstate)라 하고 n_i/N로 표현되는 차지하는 수 (occupation numbers)들의 전반적인 분포는 거시상태 (macrostate)라고 합니다. 다중성 W는 거시상태의 가중치 (the weight of the macrostate)로 알려져 있습니다.
- 무작위 이산변수 X의 상태 xi로 우리는 bin들을 p(X = xi) = pi로 해석할 수 있습니다. 랜덤 변수 X의 엔트로피는 그러면 수식 1.98과 같이 됩니다.

- 몇 가지 값들에서 피크가 생기는 분포 p(x_i)는 상대적으로 낮은 엔트로피 값을 갖습니다. 반면 넓게 분포한 경우에는 엔트로피가 상대적으로 높게 나타납니다. 이것은 그림 1.30에 나와있습니다.
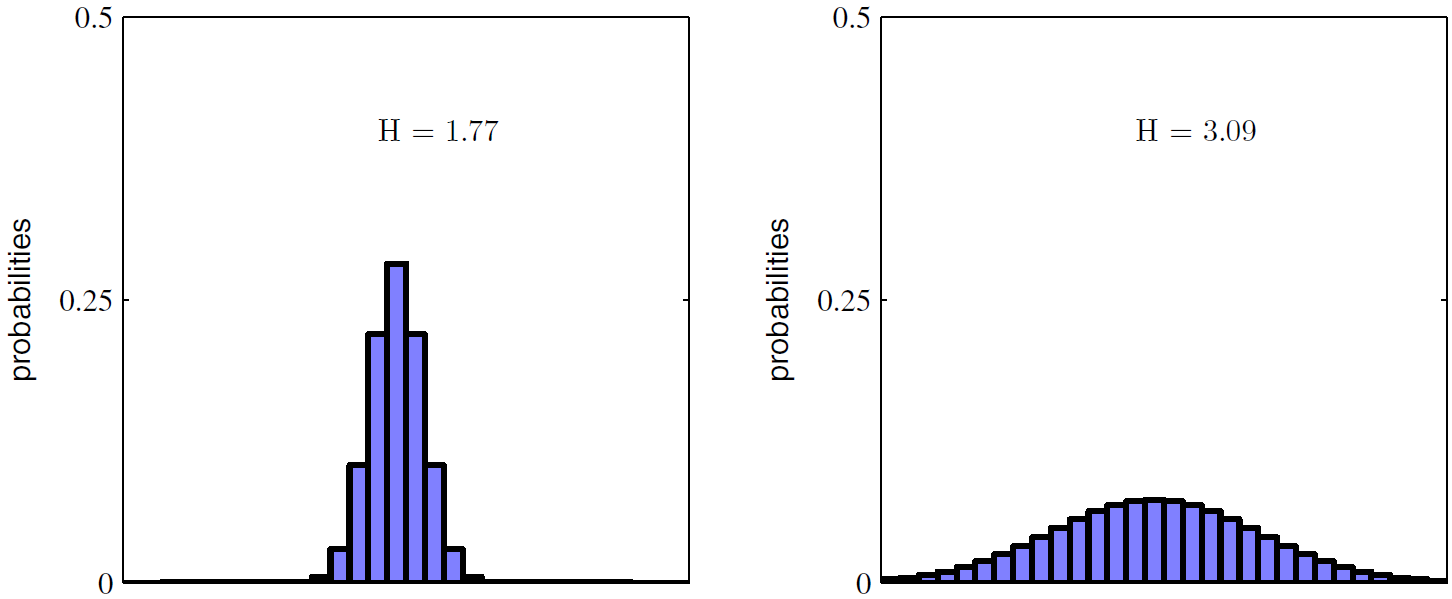
- 최대 엔트로피 구성 (maximum entropy configuration)은 확률에 대한 정규화 제약을 강제하기 위해 라그랑지 승수 (Lagrange multiplier)를 사용하여 H를 최대화함으로써 찾을 수 있습니다. (수식 1.99)
여기서 모든 p(x_i)는 같고 p(x_i)=1/M으로 주어집니다. 여기서 M은 x_i의 모든 가능한 상태의 수입니다. 엔트로피에 상응하는 값은 H = lnM입니다. 이것은 추후 다루게 될 Jensen의 비균등성 (Jensen's inequality)에서도 유도할 수 있습니다.
라그랑주 승수법(Lagrange multiplier method)은 함수의 특정 조건 아래에서 최댓값 또는 최솟값을 찾을 때 사용되는 수학적인 기법 중 하나입니다. 함수가 주어진 제약 조건 하에서 최적값을 갖는 경우, 라그랑주 승수법은 이러한 문제를 해결하는데 도움이 됩니다. 여기선 0 =< p_i =< 1과 엔트로피는 항상 양수거나 0이라는 조건이 걸려있어서 적용 가능.
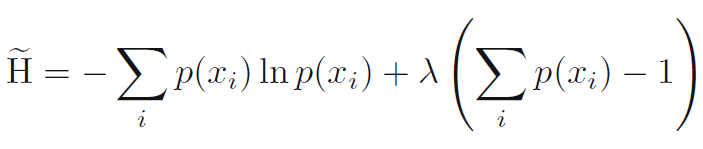
- 해당 정적인 지점에서 최대치가 되는지 확인하기 위해 우리는 엔트로피의 2차 미분 (the second derivative of the entropy)을 평가할 수 있다. 이것은 수식 1.100으로 나오며 I_ij는 정행렬 (identity matrix)이다.
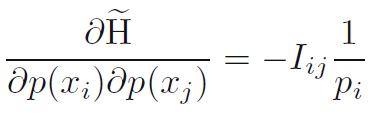
- 우리는 분포 p(x)를 연속적인 값들에대해 확장할 수 있다. 먼저 x를 폭이 delta인 집합들로 나눈다. 그리고 p(x)는 연속적이라고 가정한다. 평균값 정리 (mean value theorem)으로 이러한 각 집합에대해 x_i라는 값이 반드시 존재하므로 수식 1.101과 같이 된다.

- 이제 연속적인 값 x가 i번 째 집합에 들어가면 x_i에 배정할 수 있고 이를 통해 x를 정량화 (quantize) 할 수 있다. x_i를 관측하는 확률은 이를 통해 p(x_i)*delta가 된다. 이것은 이산적인 분포를 엔트로피에 대해 수식 1.102와 같은 식으로 표현된다. 여기서 수식 1.101을 활용해 sigma[p(x_i)*delta]는 1이다.

- 이제 수식 1.102 우변의 두 번 째 항인 -ln[delta]를 생략하고 delta->0으로 진행하자. 그러면 우변의 첫 번째 항은 p(x)ln[p(x)]의 적분 형태로 수렴하게 된다. 따라서 수식 1.103이 된다. 여기서 수식 1.103의 우변은 미분 엔트로피 (differential entropy)라 한다.

- 위의 과정을 통해 볼 수 있는 것은 이산적인 것과 연속적인 형태의 엔트로피는 ln[delta]만큼의 차이가 나는 것을 알 수 있다. 이것은 delta->0 이 될 때 발산하게 된다. 이것은 연속적인 값들을 매우 정밀하게 명시하기 (specify) 위해서는 매우 많은 bits가 필요하다는 것을 반영하는 것이다.
- 벡터 x로 정의되는 여러가지 연속적인 변수들에 대해 정의된 밀도에 대해서는 미분 엔트로피는 수식 1.104와 같이 나타난다.
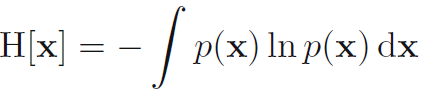
- 이산 분포 (discrete distribution)의 경우, 최대 엔트로피값은 변수들의 상태의 가능한 상황들에 대해 동일한 확률들일 때 된다는 것을 압니다. 이제 연속적인 값일 때 최대값은 어떻게 되는지 확인합시다. 이를 위해서는 p(x)의 첫 번째와 두 번 째를 제한하고 표준화 상수 (normalization constraint)를 보존해야합니다. 따라서, 우리는 미분 엔트로피 (differential entropy)를 최대화하는 것을 수식 1.105, 1.106, 그리고 1.107과 같은 3가지 제한 (constraints)을 가지고 합니다.
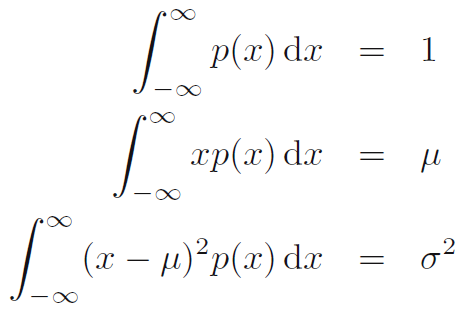
- 라그랑주 승수 (Lagrange multiplier)를 통해 제한된 최대화는 다음 함수를 p(x)에 대해 최대화하는 과정입니다. (수식 c)
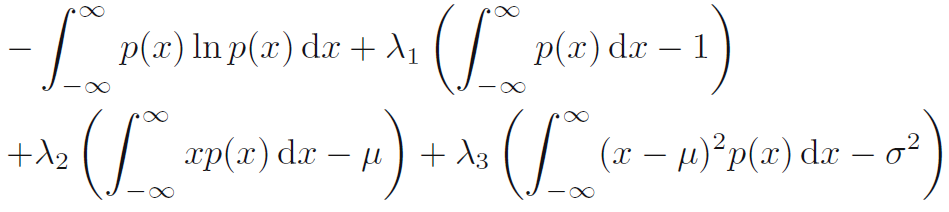
- 변분법 (calculus of variations)을 사용해서 이 도함수 (derivatice of this functional) 를 0으로 설정합니다. 이를 통해 수식 1.108이 나옵니다.
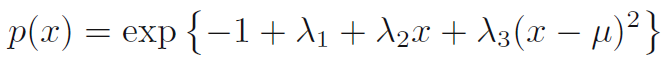
- 이 결과를 세 제약 조건 방정식에 역대입하여 라그랑지 승수를 찾을 수 있으며, 이는 마지막으로 결과 (수식 1.109)로 이끕니다. 따라서, 미분 엔트로피를 최대화하는 것은 가우시안임이 도출됩니다. 우리는 엔트로피를 최대화 시킬 때 분포를 양수에만 제한시키지 않았지만, 도출된 분포가 양수이기 때문에 나중에 깨닫게 됐지만 양수로 숫자들을 제한할 필요가 없다는 사실을 알게 됩니다.
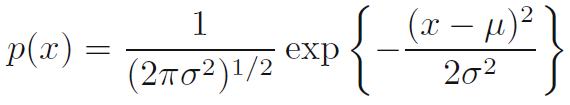
- 만일 우리가 가우시안의 미분 엔트로피를 평가한다면 우리는 수식 1.110을 얻게 됩니다. 따라서, 우리는 엔트로피가 증가하는 것은 분포가 넓어짐에 따라 증가하는 것을 볼 수 있습니다. 즉 이는 분산 (sigma**2)가 증가한다는 것을 의미합니다. 그리고 이 결과는 미분 엔트로피가 이산 엔트로피와 달리 음수가 될 수 있음을 보여줍니다. 왜냐하면 H(x) < 0은 sigma**2 < 1/(2πe) 일 때 가능하기 때문입니다.
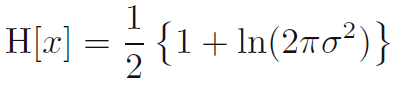
- 우리가 결합 분포 p(x,y)를 x와 y에서 각 1개씩 뽑아 가지고 있다고 합시다. 만일 x를 이미 알고 있다면, y에 상응하는 값을 구체화하기 위해 추가적으로 필요한 정보는 -ln[p(y|x)]로 주어집니다. 따라서, y를 구체화하기위한 평균적인 정보는 수식 1.111과 같이 표현됩니다. 이를 주어진 x에 대한 y의 조건부 엔트로피 (conditional entropy)라고 합니다.
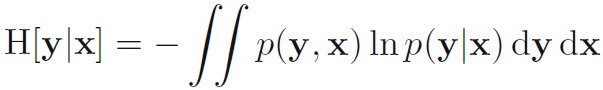
- 곱셈 법칙을 활용하면 조건부 엔트로피는 수식 1.112를 만족하는 것을 알 수 있습니다.
여기서 H[x,y]는 p(x,y)의 미분 엔트로피이고 H[x]는 주변 분포 (marginal distribution) p(x)의 미분 엔트로피입니다. 따라서, x와 y를 기술하기 위한 정보는 x를 기술하기 위한 정보와 x가 주어졌을 때 y를 기술할 정보를 더하면 됩니다.
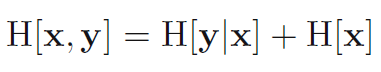
728x90
반응형
'DeepLearning > Pattern recognition and Machine learning' 카테고리의 다른 글
| [PRML] 2. Probability distributions (확률 분포들) (0) | 2024.01.26 |
|---|---|
| [PRML] 1.6.1 Relative entropy and mutual information (상대 엔트로피와 상호 의존 정보) (0) | 2024.01.23 |
| [PRML] 1.5.5 Loss functions for regression (회귀에 대한 손실함수들) (0) | 2024.01.12 |
| [PRML] 1.5.4 Inference and decision (추론과 결정) (0) | 2024.01.11 |
| [PRML] 1.5.3 The reject option (거부 옵션) (0) | 2024.01.11 |


